Proof, Computation and Truth
I want to investigate the nature of and limits of mathematics. To do that, I'll explore logic, set theory, computability, information theory and philosophy. Be warned that this essay is rather long; it starts relatively easy and gets significantly harder. I hope everyone will get something out of it (including my tutors!) but if you're new to mathematics, that might not be much. If you're philosophically inclined, definitely look at the last section on Truth and Induction. Any discussion or errata are of course very welcome.
Let's start with some historical background. Although the Babylonians were able to do some interesting calculations (particularly astronomical), mathematics in the sense of deductive arguments from premises to conclusions began with Thales, Pythagoras and their disciples. Greek maths was focused on geometry, which was formalised by Euclid into 5 axioms - foundational assertions - from which he proved many theorems. Euclidean geometry (as formalised more rigorously by Tarski) has a few interesting properties. Firstly, it is consistent: there is no way to derive a contradiction from the axioms. Secondly, it is decidable: there is an algorithm which, for any geometrical statement, decides whether it has a correct proof or not. Thirdly, it is complete: every geometric statement can either be proved or disproved from the axioms. Fourthly, it is false in the real world (in an intuitive sense; describing rigorously what that means is incredibly difficult). We now know, thanks to Einstein's relativity, that space is not flat and therefore we need to use a different version of geometry to model it properly.
It's important to thoroughly understand the properties above, and how they relate to each other in general. For example:
Would the 3rd system be decidable as well? We can't answer this yet, because the explanations so far have skimmed over a few important things. Firstly, how do we know, rigorously, which proofs are correct and which aren't? Secondly, what do we mean by statements - can they include words, numbers, symbols? Thirdly, how can we interpret statements without any ambiguity?
Logic
The answer is that we encode each statement and proof in a logical language; we can only trust the edifice of mathematics which we are about to build up as much as we trust the rules of that language. The key things to know are that logical statements are purely symbolic, and logical proofs consist of branching chains of statements. Importantly, each link in the chain must be generated by one of a few strict rules, which are chosen to be as obvious as possible (for example, from the statement A ∧ B, meaning that A and B are both true, there is a rule allowing us to derive the statement A, meaning that A is true). The only statements which do not need to be generated by those rules are the axioms. If a valid proof finishes in a statement, then it proves that statement. The simplest form of logic is called propositional logic, which lets us form statements out of propositions (which can be either true or false, and are represented by uppercase letters) joined by the connective symbols ∧ (AND), ∨ (OR), ~ (NOT) and → (IMPLIES). The truth-value of a statement depends on the truth-values of its constituent propositions and which connectives are used. For example, ~A ∨ B is false if A is true and B is false, and true otherwise. It is important to note that the meaning of propositions is not defined within the language itself, but rather is a matter of interpretation: the statement P could mean anything I want; the statement P ∧ Q could mean any two things I want.
Propositional logic is very weak (because sentences such as "There is a man named Socrates" can only be treated as a single proposition, not broken up into components) and so we more commonly use first-order predicate logic (L1). This is the same as propositional logic, but as well as propositions we have variables which range over some (implicit) domain. We reason about objects in that domain using existential and universal quantifiers ∃ (meaning "there exists") and ∀ (meaning "for all") and "predicates" (which are essentially just functions). So for example, we're now able to translate our previous axiom "There is a man named Socrates" as ∃x(Mx ∧ Sx): "there exists something which is a man and is named Socrates". Here M is a predicate which outputs true when its input is a man, and S is a predicate which outputs true when its input is named Socrates. Similarly, "Socrates is the only man" can be represented as ∃x(Mx ∧ Sx ∧ ∀z(Mz → z=x)): "there exists something which is a man and is named Socrates, and anything else being a man implies that they're the same thing". In a system with this as the only axiom - call it the S-system - you could prove a number of statements such as ∃x(Mx) (interpreted as "There is at least one man") and ∀x(Mx → Sx) ("Every man is named Socrates"). However, you could also prove infinitely many other things which have nothing to do with men or Socrates! Remember that a proof is simply a chain of statements which is generated according to certain rules - it doesn't have to use any of the axioms. So every statement which can be proved without reference to any axiom can be proved in the S-system - for example, P∨~P. Such statements are true under any interpretation - no matter what you take P to mean, for example, P∨~P will still hold. Unfortunately, this proliferation of theorems makes the S-system, and all other consistent L1 systems, undecidable.
I stress again that, although the correctness of a proof can be seen just by looking at the structure of each statement in it, the English meaning of L1 statements can't be determined by the propositions and predicates alone, but rather requires some interpretation of what they represent. This is why we're able to make statements about Socrates: when doing so, we take the domain to be all people, or perhaps all objects, of which Socrates is one. When we're doing Euclidean geometry, by contrast, we might take the domain to be all points, lines and planes (this will vary by how we choose to formalise Euclidean geometry, since Euclid obviously wasn't able to write his axioms in L1). In my discussion of Euclidean geometry above, I was using properties of Tarski's formulation, which has a domain consisting only of individual points. Modern mathematics is also based on a domain with only one type of object; we call them sets.
(Higher-order predicate logics allow us to quantify over predicates themselves - so that in second-order predicate logic we can talk about the properties of predicates, and in third-order predicate logic we can talk about the properties of the properties of predicates. However, these aren't nearly as useful as first-order predicate logic.)
Set theory
In the 19th century, maths was expanding greatly, and its various branches made use of strange entities such as infinities, infinitesimals, and fractal functions. Mathematicians wanted to be sure that all of these "made sense" and could fit together; and so set theory was developed in order to provide a proper foundation for all mathematics. The version of set theory which is currently used, ZF, was developed by Zermelo and Frankel: it contains 8 axioms. They are all formulated in L1, using only the predicates "is an element of" (∈) and "equals" (=). I'll also use A⇔B as a shorthand for (A → B)∧(B → A). Let's look at a few of them. The first axiom is that an empty set exists. We can write this: ∃x(~∃y(y∈x)): "there exists something such that there doesn't exist anything which is an element of it". See again how the axiom shows that something exists, and we choose to call this a set. The second axiom asserts that two sets are equal if and only if they contain exactly the same elements; we write it ∀x∀y∀z((z∈x⇔z∈y) → x=y): "for all pairs of things, if something being in one implies that it's in the other, then that pair is equal". The third axiom, the axiom of pairs, states that if x and y are sets, then there exists a set which contains x and y as elements. Have a shot at formulating this in L1 yourself; the answer is at the very bottom.
And so on it goes, with more axioms adding more power to our system of mathematics. Two more of the standard axioms deserve particular mention. The first is the axiom of comprehension, which states: for any set S, and any property P which can be formulated in L1, then there is a set containing exactly all the elements of S which satisfy P. This is also known as "restricted comprehension", because it is a less powerful version of a previous axiom which had been suggested: that for any property P which can be formulated in L1, there is a set containing exactly all the sets which satisfy P. But this leads to a contradiction, by considering the property of "not containing itself" (for a set s, simply ~s∈s). Let N be the set of all sets which do not contain themselves. Then does N contain itself? If so, then it should not contain itself; but if not, then it should. Therefore the axiom makes ZF inconsistent. After this paradox threatened to undermine the basis of set theory, restricted comprehension was adopted instead; now neither N nor the set of all sets can exist.
The second interesting axiom is the axiom of infinity, which allows us for the first time to make the jump into infinite sets. To specify this axiom, we first need the concept of ordinal numbers, which we define inductively. 0 is represented as the empty set, {}; then the successor of any set s is represented as s U {s}. For example, 1 is {} U {{}} = {{}}, 2 is {{}} U {{{}}} = { {}, {{}} }. Note that each ordinal number contains all previous numbers as subsets. Now we define an inductive set to be one which contains the empty set, plus the successor of every element in the set. The axiom of infinity states that an inductive set exists. Then the set of all natural numbers - call it w - must be a subset of it.
A consequence of the existence of w is that we can now define infinite ordinals. Consider the successor of w: w U {w}. This contains w itself as a strict subset, and thus represents the next number "larger" than w, which is w+1. Using other axioms we can keep applying the successor function to get w+w, w^2, and eventually w^w and even uncountable ordinals. This illustrates the difference between ordinals, which represent some ordering of sets of numbers, and cardinals, which represent the magnitudes of such sets. For example, we can picture the ordinal w+1 as all the natural numbers on a number line, and then after they have all finished, another 1: 1,2,3...,1. Meanwhile w+w is every natural number, followed by another copy of the natural numbers: 1,2,3,...,1,2,3,... By contrast, the cardinality of each of these is exactly the same as the cardinality of w, since they can be put into bijection with each other.
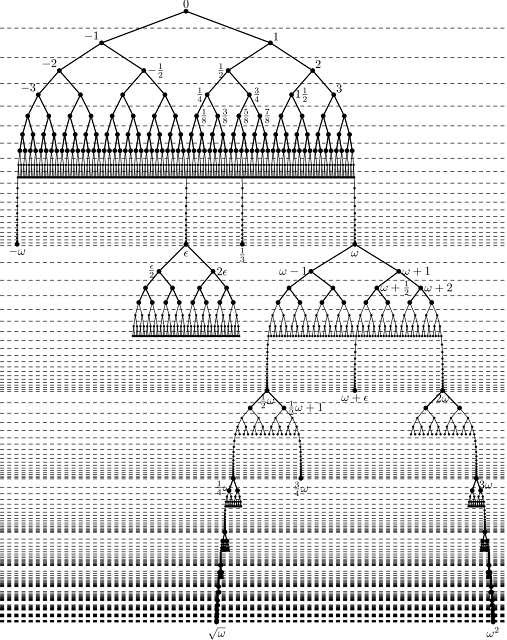
From ordinals representing the non-negative integers, we can define all integers as ordered pairs of a positive integer and a "sign" represented by 0 or 1; then we define rationals as ordered pairs of integers. Real numbers are represented using "Dedekind cuts", i.e. for each real number the unique subset of all rational numbers which are strictly less than it. I want to note that these are not the only way to define numbers within set theory. Indeed, these constructions have been criticised as rather arbitrary, especially in comparsion with the Surreal Numbers, which were independently rediscovered multiple times, including by Conway as a result of investigating the endgame of the game of Go! The surreal number system, from one simple construction (the pair operation), defines all integers, rationals and reals as well as infinitesimals and all infinite ordinals. The easiest way to explain is probably with the image below. 0 is defined as the empty pair, {|}; 1 is {0|}; 1/2 is {0|1} and so on. Rationals with powers of 2 in the denominator are defined as the pair of any two numbers that they're equidistant between; all other rationals and reals are limits of pair operations over the rationals already defined. The downside of the surreal numbers is that they still require a (limited) form of set theory to reason about what happens after infinitely many operations; so they aren't able to provide a full alternative to it.
At this point our axioms seem quite powerful. Assuming that they're consistent, we might hope to be able to use them to prove every arithmetic statement which can be encoded in L1 either true or false - that is, we hope the axioms are complete. However, this hope is dashed by Godel's First Incompleteness Theorem, which states that in any consistent system powerful enough to represent arithmetic, there are some true statements unprovable by the system. He proves this by constructing a self-referential statement which negates its own provability; then if it false, it can be proved, which is impossible; therefore it must be true and unprovable.
You might object at this point (as Roger Penrose has been doing for some time) that if we can know that the "unprovable" statement is true, then we must have proved it mentally. However, we only know that it is true because we have assumed that ZF is consistent! By doing so, we are going beyond the ZF axioms and reasoning in an informal "meta-language". If we tried to formalise that meta-language, we know that the resulting system would have Godellian true-but-unprovable statements, and we wouldn't ever be able to figure out what they were (without making further assumptions)! So there's not much point in doing so.
Godel's construction is an obscure one, but other examples of true statements unprovable from the ZF axioms were soon found. In particular, the Axiom of Choice and the Continuum Hypothesis are both independent from ZF: that is, ZF can neither prove that they are true or that they are false. If we assume that every mathematical statement must be either true or false, either these statements or their negations are true and unprovable in ZF. The Axiom of Choice is interesting because it is equivalent to Cardinal Comparability, which seems to be "clearly true"; but also to the Well-Ordering Principle, which seems "clearly false"; and also to Zorn's lemma, which is somewhere in the middle. Most mathematicians now accept the axiom of choice, adding it to the Zermelo-Frankel axioms to give the ZFC system.
We next wonder about consistency itself: it would be great to prove that our ZF axioms are at least consistent if not complete. However, Godel's Second Incompleteness Theorem shows that no consistent system powerful enough to represent arithmetic can prove its own consistency. If it could, then it would be able use the same reasoning that we did in arguing that the self-referential statement from the First Incompleteness Theorem was true, which would make that statement provable after all! We can of course prove the consistency of ZF set theory given some other assumptions - but then we wouldn't be able to prove the consistency of ZF + other assumptions without still more assumptions, and so on (assuming each addition maintains consistency). The best we can hope for here is an appeal to how obvious the axioms are in our universe. In any case, this theorem gives us another example of a (hopefully) true but unprovable statement: the statement of ZF's consistency.
Computability
At this point (in the 1930s) mathematicians were feeling rather dispirited, but there was one last property which they still hoped for: decidability. That is, even though ZF was incomplete, was there any algorithm which would solve Hilbert's "entscheidungsproblem" of deciding in a finite time whether any given statement was provable or not? This problem relied, however, on a definition of algorithm, which was provided independently by Church, Godel and Turing, using entirely different formulations which happened to be equivalent. The equivalence of lambda calculus, u-recursive functions and many different formulations of Turing machines strongly suggests that there is some "natural" divide between questions which can be decided by algorithms and those which can't - and unfortunately for mathematicians, the provability of some mathematical statements is in the latter category. Turing showed this by demonstrating that any algorithm which could figure out whether any Turing Machine halted eventually could produce a contradiction when applied to a version of itself (the role of self-reference in his, Godel's and other impossibility proofs is fascinating!). A follow-up theorem from Rice showed that in fact every non-trivial semantic property of Turing machines is undecidable, because they can be reduced to the halting problem. Turing Machines are limited in other ways too: since there are only a countable infinity of Turing machines and an uncountable infinity of real numbers, "almost every" number is uncomputable, in the sense that there is no Turing machine which outputs it. However, in another sense Turing Machines are an incredibly powerful construction: they can run for arbitrarily long and take up arbitrarily large amounts of space. Further, Universal Turing Machines exist which can simulate any other Turing Machine given to them as input. It is an open empirical question whether or not Turing Machines describe every computation possible in our universe: so far it seems they do, with two caveats. Firstly, Turing Machines are not able to generate true randomness, and so if quantum mechanics is nondeterministic, it could not be implemented using a Turing Machine. However, pseudorandomness is good enough for all practical purposes. Secondly, quantum computers are able to perform some calculations faster than any Turing Machine - but not, it seems, any calculation which a Turing Machine couldn't do eventually.
Since Turing Machines are so important, I'll give a brief sketch of what they are. Turing based his theory of computation on a human mathematician working with pen and paper. The Turing Machine consists of an infinitely long tape, divided into squares which can contain one symbol each - initially they are all empty except for a finite amount of input. There is also a "head" which moves back and forth over the tape one square at a time, reading the symbol there, possibly rewriting it, and possibly changing state. Each state has its own rules for what to do when reading each symbol, and which states it may transition into. Turing argued that because any human mathematician can only distinguish between finitely many symbols, and only remember finitely many things, the symbols and states for each Turing Machine should also be finite. Eventually the Turing Machine may reach a "halting state"; the contents of the tape at that time are the output. Otherwise, the computation may simply never finish. We can relate Turing Machines to mathematics as follows: we define a mathematical system to be a Turing Machine which, given a list of axioms and a mathematical statement (both in L1) either outputs a proof of the statement from the axioms, or else runs forever. Thus we must build the rules of logic into the Turing machine, but the rules of the mathematical system can vary depending on which axioms are used. Of course, from Gödel we know that there are some true statements on which such a machine will run forever.
In fact, using this definition, we can actually come up with more statements which are true but unprovable. Assume that ZF is consistent. Now consider the statement "All Turing machines with n states either halt in fewer than k steps, or run forever." For every value of n, there are only finitely many Turing machines, and so there must be some least value of k for which the statement is true (we assume they start on a blank tape). This value is called the nth Busy Beaver number, or BB(n). But what if n = N, where N is large enough for there to be a N-state Turing machine which searches for a contradiction in ZF by listing all possible proofs and stopping if it finds a proof of a contradiction? Then it cannot halt, because ZF is consistent. But if ZF could prove what BB(N) was, then running it for BB(N) steps without it halting would be a proof that it never halted and that ZF is consistent, which is impossible by Godel's Second Incompleteness Theorem. Thus the value of BB(N) can never be proved in ZF.
What sort of sizes of N are we talking about here? Yedida and Aaronson prove an upper bound on which Busy Beaver numbers can ever be found - it's around 8000 in a variant of ZF which includes a large cardinal axiom. Notice that it must be large enough for a N-state Turing Machine to implicitly encode all the axioms of ZF, plus encode the algorithm for listing and checking all proofs from some axioms. The latter only takes a constant amount of space, and so it turns out that the more compactly our axioms can be encoded, the less we can prove with them! This suggests a fundamental connection between information and proof, one which has been explored in recent decades by the field of algorithmic information theory.
Algorithmic information theory
Algorithmic information theory uses a slightly different convention when it comes to information (following Shannon, who singlehandedly founded information theory in 1948). "Turing Machine states" is not a very natural unit to use for how much information a set of axioms contains; rather, we usually talk about information in terms of "bits". Each bit of information we receive narrows the options we're considering by half. For example, if you wanted to send me a string of 4 binary digits, there are 16 possibilities - but once I receive the first digit, then there are only 8 possibilities left for the remaining 3 digits, so I've received 1 bit of information. Note, though, that "half" is not measured in number of outcomes, but rather in the probability we assign to those outcomes. If I think there's a 50% probability the message will be 0000, 25% probability that it will be 0001, and 25% probability that it will be 1000, then receiving the digit 0 gives me less than 1 bit of information because it only rules out 25% of my initial probability distribution (specificially, it gives me -log(0.75) = 0.415 bits of information). The next two digits I receive will each give me 0 bits of information, and then the last will give me either 0.585 or 1.585 bits depending on whether it's 0 or 1.
This will be confusing for computer scientists, who are accustomed to thinking of each binary digit as 1 bit, regardless of what it is. The distinction to keep in mind is between bits of message, and bits of information. Above, we transmitted 4 bits of message but conveyed only 1 or 2 bits of information because we chose a shoddy encoding which wasted the middle two bits. The distinction makes sense. For example, if you knew I was going to send you a million-bit string of either all 0s or all 1s, then it would contain a million bits of message, but only 1 bit of information: everything after the first digit is redundant. Above we can also see that it's possible for one bit of message to contain more than 1 bit of information; another example would be if you picked a random number between 0 and 1000 and sent it to me using the following encoding: if the number is 20, then send the digit 1, otherwise send 0 followed by the actual number. If I receive a 1, you've ruled out 0.999 of the probability, and given me almost 10 bits of information, with only 1 bit of message. The catch which Shannon proved is that, on average, you can never expect to receive more than 1 bit of information with every bit of message: for every time our unusual encoding scheme saves us effort, there will be 999 times when it adds an unnecessary bit on to the message.
Chaitin has a cool proof of Godel's incompleteness theorem inspired by algorithmic information theory. He notes that Godel's original proof is based on the classic paradox "This sentence is a lie" - except with untruth replaced by unprovability. He bases his proof on another well-known paradox: "The smallest number which cannot be specified in fewer than 100 words." Since there are only finitely many strings of fewer than 100 words, there must be such a number. But whatever it is, we've just specified it in 12 words, so it cannot exist! Formally: given a fixed language, let the complexity of a number be the length of the shortest description of a Turing machine which gives it as output. Consider the number which is defined as follows: search through all possible proofs, in order of length, and identify the ones which demonstrate that a number has a complexity greater than N; output the number which has the shortest such proof. But if N is bigger than the description length required to encode all the axioms and the operating instructions for the Turing Machine I described above, then the program we just described above will have length < N, and so the number we found actually has complexity < N. Contradiction! Therefore we can never prove the complexity of numbers above a certain threshold; and that threshold is based on how many bits of information are contained in the axioms in the language we're using! Chaitin also demonstrated the same idea by formulating "Chaitin's constant", Ω, defined as an exponentially weighted sum of all Turing Machines. Each Turing Machine of length n adds 1/2^n to Ω if it halts, and 0 otherwise. Then Ω can be seen as the probability that a randomly chosen Turing Machine halts. If we know the first K bits of Ω, then we can solve the Halting Problem for all Turing Machines of length < K, by running all other Turing Machines in parallel, adding together the weighted sum of those which have halted, and waiting for that sum to come close enough to Ω that any Turing Machine of length < K halting would push the sum past Ω. Because of this, Ω is uncomputable; further, by a similar argument to the used above with the Busy Beaver numbers, every system of axioms has some upper limit beyond which it cannot determine the digits of Ω. That upper limit is the information content of the axioms, measured in bits, plus a constant which depends on the encoding language we are using.
These results lead Chaitin to a novel view of mathematics. Instead of maths being fundamentally about building up knowledge from axioms, he argues that we should accept that we can prove strictly more if we add more axioms. Therefore mathematicians should behave more like physicists: if there is an elegant, compelling statement which is supported by evidence like numerical checking, but which we haven't been able to prove despite significant effort, then we should simply add it as an axiom and carry on. To some extent, mathematicians have been doing this with the Axiom of Choice, Continuum Hypothesis and large cardinal axioms - the difference is that these are almost all known to be independent from ZF, whereas Chaitin advocates adding working axioms even without such knowledge. Whether or not this is a useful proposal, it is certainly interesting to consider which the major unsolved problems - the Navier-Stokes equations, P = NP, the Hodge Conjecture - may in fact be independent of ZF. And that question brings us to the last part of this discussion, centered around truth in the empirical world.
Truth and Induction
Are our mathematical axioms true? That's a dangerous question. What could it mean, in a universe of atoms and energy, for a mathematical theory to be true? That physical objects obey mathematical rules? We used to think that all objects implemented arithmetic relations: if you have one, and add another, then you end up with two. Now we know that objects are wavefunctions which don't add in such simple ways - and yet nobody thinks that this reflects badly on arithmetic. Is it that physical laws can be very neatly described using mathematics? In that case, what about axioms which aren't needed to describe those laws? Chaitin created a series of exponential diophantine equations which have finitely many solutions only if the corresponding digit of Ω is 0 - so we can never know whether they do or not without many bits of new axioms. But diophantine equations are just addition and multiplication of integers, and surely if anything has some objective truth then it is the outcomes of these basic equations. Now consider a more abstract axiom like the Continuum Hypothesis: either it's true, or it's not true - or we can no longer rely on the logical law of P ∨ ~P. But if it's true, what on earth makes it true? How would the universe possibly be different if it were false? For most of the last two millennia, mathematicians have implicitly accepted Plato's idealisation of numbers "existing" in a realm beyond our own - but with the developments in mathematics that I outlined above, that consensus doesn't really stand up any more. Perhaps we should take Kronecker's intuitive approach - "God made the natural numbers; all else is the work of man" - but if that's true, why does "all else" work so well in physics? On the other hand, Quine advocated only believing in the truth of mathematics to the extent that its truth was a good explanation for our best scientific theories - given current theories, that implies that we should stop roughly at the point where we've derived fields of complex numbers. Even so, what does it mean to believe that the complex or even real numbers "exist"?
I'm going to bow out of answering these questions, because I haven't actually taken any courses on the philosophy of mathematics; I'm hoping that some readers will be able to contribute more. For those interested in exploring further, I recommend a short paper called The Unreasonable Effectiveness of Mathematics in the Natural Sciences. However, now that we've ventured back into the real world, there is one more important issue to discuss: how can we draw conclusions about the world given that, in principle, anything could be possible? We could be in the Matrix - you could all be zombies - the laws of physics could change overnight - the Sun could stop shining tomorrow: these are the problems of induction and skepticism which has plagued philosophers for centuries. In recent decades many philosophers have subscribed to Bayesianism, a framework for determining beliefs which I'll discuss in detail in a forthcoming post. For now, the most important feature of Bayesianism is that it requires a prior evaluation of every possibility, which must give us a consistent set of probabilities, Once we have this prior, then there is a unique rational way to change your beliefs based on any incoming evidence. However, it's very difficult to decide what the prior "should" be - leaving Bayesians in the uncomfortable position of having to defend almost all priors as equally worthy. Enter algorithmic game theory, which allows us to define the prior probability of any sequence of observations as follows. For every Turing Machine of length n, add a probability of 1/2^n to whichever sequence of observations is represented by its output. The sum of all these probabilities for Turing Machines of every length is the unique "rational" prior; the process of generating it is called Solomonoff Induction.
There are three points to make here. The first is that this solution assumes that we should assign probability 0 to any uncomputable observation (which doesn't seem unreasonable); and further, that computable observations should be discounted if they are very complicated to specify. This is an interpretation of Occam's razor - it will give philosophical purists indigestion, but I think we should recognise that going from a broad statement favouring "simplicity" to a precise computational ideal is a clear improvement. Secondly, the exact prior will depend on what language we use to encode observations. There are plenty of pathological languages which artificially place huge probability on very strange outcomes. However, as long as the language is able to encode all possible observations, then with enough evidence ideal Bayesians will converge on the truth. Thirdly, Solomonoff Induction takes infinitely long to compute, so it is only an ideal. Developing versions of it which are optimal given space and time constraints is an important ongoing project pursued by MIRI and other organisations.
That's all, folks. Congratulations for making it to the end; and since you've come this far, do drop me a line with your thoughts :) Answer to the set theory question is ∀x∀y∃z(x∈z ∧ y∈z).
Let's start with some historical background. Although the Babylonians were able to do some interesting calculations (particularly astronomical), mathematics in the sense of deductive arguments from premises to conclusions began with Thales, Pythagoras and their disciples. Greek maths was focused on geometry, which was formalised by Euclid into 5 axioms - foundational assertions - from which he proved many theorems. Euclidean geometry (as formalised more rigorously by Tarski) has a few interesting properties. Firstly, it is consistent: there is no way to derive a contradiction from the axioms. Secondly, it is decidable: there is an algorithm which, for any geometrical statement, decides whether it has a correct proof or not. Thirdly, it is complete: every geometric statement can either be proved or disproved from the axioms. Fourthly, it is false in the real world (in an intuitive sense; describing rigorously what that means is incredibly difficult). We now know, thanks to Einstein's relativity, that space is not flat and therefore we need to use a different version of geometry to model it properly.
It's important to thoroughly understand the properties above, and how they relate to each other in general. For example:
- A system which included as axioms every possible statement would be complete and decidable, but inconsistent and false.
- A system which is complete, and for which there is an algorithm which enumerates every correct proof, must also be decidable: simply run the proof-enumerating algorithm, and stop when it reaches either the statement you want to prove or its negation, which must happen eventually.
- A system which only had one axiom, reading "There is a man named Socrates", would be consistent and true, but definitely not complete.
Logic
The answer is that we encode each statement and proof in a logical language; we can only trust the edifice of mathematics which we are about to build up as much as we trust the rules of that language. The key things to know are that logical statements are purely symbolic, and logical proofs consist of branching chains of statements. Importantly, each link in the chain must be generated by one of a few strict rules, which are chosen to be as obvious as possible (for example, from the statement A ∧ B, meaning that A and B are both true, there is a rule allowing us to derive the statement A, meaning that A is true). The only statements which do not need to be generated by those rules are the axioms. If a valid proof finishes in a statement, then it proves that statement. The simplest form of logic is called propositional logic, which lets us form statements out of propositions (which can be either true or false, and are represented by uppercase letters) joined by the connective symbols ∧ (AND), ∨ (OR), ~ (NOT) and → (IMPLIES). The truth-value of a statement depends on the truth-values of its constituent propositions and which connectives are used. For example, ~A ∨ B is false if A is true and B is false, and true otherwise. It is important to note that the meaning of propositions is not defined within the language itself, but rather is a matter of interpretation: the statement P could mean anything I want; the statement P ∧ Q could mean any two things I want.
Propositional logic is very weak (because sentences such as "There is a man named Socrates" can only be treated as a single proposition, not broken up into components) and so we more commonly use first-order predicate logic (L1). This is the same as propositional logic, but as well as propositions we have variables which range over some (implicit) domain. We reason about objects in that domain using existential and universal quantifiers ∃ (meaning "there exists") and ∀ (meaning "for all") and "predicates" (which are essentially just functions). So for example, we're now able to translate our previous axiom "There is a man named Socrates" as ∃x(Mx ∧ Sx): "there exists something which is a man and is named Socrates". Here M is a predicate which outputs true when its input is a man, and S is a predicate which outputs true when its input is named Socrates. Similarly, "Socrates is the only man" can be represented as ∃x(Mx ∧ Sx ∧ ∀z(Mz → z=x)): "there exists something which is a man and is named Socrates, and anything else being a man implies that they're the same thing". In a system with this as the only axiom - call it the S-system - you could prove a number of statements such as ∃x(Mx) (interpreted as "There is at least one man") and ∀x(Mx → Sx) ("Every man is named Socrates"). However, you could also prove infinitely many other things which have nothing to do with men or Socrates! Remember that a proof is simply a chain of statements which is generated according to certain rules - it doesn't have to use any of the axioms. So every statement which can be proved without reference to any axiom can be proved in the S-system - for example, P∨~P. Such statements are true under any interpretation - no matter what you take P to mean, for example, P∨~P will still hold. Unfortunately, this proliferation of theorems makes the S-system, and all other consistent L1 systems, undecidable.
I stress again that, although the correctness of a proof can be seen just by looking at the structure of each statement in it, the English meaning of L1 statements can't be determined by the propositions and predicates alone, but rather requires some interpretation of what they represent. This is why we're able to make statements about Socrates: when doing so, we take the domain to be all people, or perhaps all objects, of which Socrates is one. When we're doing Euclidean geometry, by contrast, we might take the domain to be all points, lines and planes (this will vary by how we choose to formalise Euclidean geometry, since Euclid obviously wasn't able to write his axioms in L1). In my discussion of Euclidean geometry above, I was using properties of Tarski's formulation, which has a domain consisting only of individual points. Modern mathematics is also based on a domain with only one type of object; we call them sets.
(Higher-order predicate logics allow us to quantify over predicates themselves - so that in second-order predicate logic we can talk about the properties of predicates, and in third-order predicate logic we can talk about the properties of the properties of predicates. However, these aren't nearly as useful as first-order predicate logic.)
In the 19th century, maths was expanding greatly, and its various branches made use of strange entities such as infinities, infinitesimals, and fractal functions. Mathematicians wanted to be sure that all of these "made sense" and could fit together; and so set theory was developed in order to provide a proper foundation for all mathematics. The version of set theory which is currently used, ZF, was developed by Zermelo and Frankel: it contains 8 axioms. They are all formulated in L1, using only the predicates "is an element of" (∈) and "equals" (=). I'll also use A⇔B as a shorthand for (A → B)∧(B → A). Let's look at a few of them. The first axiom is that an empty set exists. We can write this: ∃x(~∃y(y∈x)): "there exists something such that there doesn't exist anything which is an element of it". See again how the axiom shows that something exists, and we choose to call this a set. The second axiom asserts that two sets are equal if and only if they contain exactly the same elements; we write it ∀x∀y∀z((z∈x⇔z∈y) → x=y): "for all pairs of things, if something being in one implies that it's in the other, then that pair is equal". The third axiom, the axiom of pairs, states that if x and y are sets, then there exists a set which contains x and y as elements. Have a shot at formulating this in L1 yourself; the answer is at the very bottom.
And so on it goes, with more axioms adding more power to our system of mathematics. Two more of the standard axioms deserve particular mention. The first is the axiom of comprehension, which states: for any set S, and any property P which can be formulated in L1, then there is a set containing exactly all the elements of S which satisfy P. This is also known as "restricted comprehension", because it is a less powerful version of a previous axiom which had been suggested: that for any property P which can be formulated in L1, there is a set containing exactly all the sets which satisfy P. But this leads to a contradiction, by considering the property of "not containing itself" (for a set s, simply ~s∈s). Let N be the set of all sets which do not contain themselves. Then does N contain itself? If so, then it should not contain itself; but if not, then it should. Therefore the axiom makes ZF inconsistent. After this paradox threatened to undermine the basis of set theory, restricted comprehension was adopted instead; now neither N nor the set of all sets can exist.
The second interesting axiom is the axiom of infinity, which allows us for the first time to make the jump into infinite sets. To specify this axiom, we first need the concept of ordinal numbers, which we define inductively. 0 is represented as the empty set, {}; then the successor of any set s is represented as s U {s}. For example, 1 is {} U {{}} = {{}}, 2 is {{}} U {{{}}} = { {}, {{}} }. Note that each ordinal number contains all previous numbers as subsets. Now we define an inductive set to be one which contains the empty set, plus the successor of every element in the set. The axiom of infinity states that an inductive set exists. Then the set of all natural numbers - call it w - must be a subset of it.
A consequence of the existence of w is that we can now define infinite ordinals. Consider the successor of w: w U {w}. This contains w itself as a strict subset, and thus represents the next number "larger" than w, which is w+1. Using other axioms we can keep applying the successor function to get w+w, w^2, and eventually w^w and even uncountable ordinals. This illustrates the difference between ordinals, which represent some ordering of sets of numbers, and cardinals, which represent the magnitudes of such sets. For example, we can picture the ordinal w+1 as all the natural numbers on a number line, and then after they have all finished, another 1: 1,2,3...,1. Meanwhile w+w is every natural number, followed by another copy of the natural numbers: 1,2,3,...,1,2,3,... By contrast, the cardinality of each of these is exactly the same as the cardinality of w, since they can be put into bijection with each other.
From ordinals representing the non-negative integers, we can define all integers as ordered pairs of a positive integer and a "sign" represented by 0 or 1; then we define rationals as ordered pairs of integers. Real numbers are represented using "Dedekind cuts", i.e. for each real number the unique subset of all rational numbers which are strictly less than it. I want to note that these are not the only way to define numbers within set theory. Indeed, these constructions have been criticised as rather arbitrary, especially in comparsion with the Surreal Numbers, which were independently rediscovered multiple times, including by Conway as a result of investigating the endgame of the game of Go! The surreal number system, from one simple construction (the pair operation), defines all integers, rationals and reals as well as infinitesimals and all infinite ordinals. The easiest way to explain is probably with the image below. 0 is defined as the empty pair, {|}; 1 is {0|}; 1/2 is {0|1} and so on. Rationals with powers of 2 in the denominator are defined as the pair of any two numbers that they're equidistant between; all other rationals and reals are limits of pair operations over the rationals already defined. The downside of the surreal numbers is that they still require a (limited) form of set theory to reason about what happens after infinitely many operations; so they aren't able to provide a full alternative to it.
You might object at this point (as Roger Penrose has been doing for some time) that if we can know that the "unprovable" statement is true, then we must have proved it mentally. However, we only know that it is true because we have assumed that ZF is consistent! By doing so, we are going beyond the ZF axioms and reasoning in an informal "meta-language". If we tried to formalise that meta-language, we know that the resulting system would have Godellian true-but-unprovable statements, and we wouldn't ever be able to figure out what they were (without making further assumptions)! So there's not much point in doing so.
Godel's construction is an obscure one, but other examples of true statements unprovable from the ZF axioms were soon found. In particular, the Axiom of Choice and the Continuum Hypothesis are both independent from ZF: that is, ZF can neither prove that they are true or that they are false. If we assume that every mathematical statement must be either true or false, either these statements or their negations are true and unprovable in ZF. The Axiom of Choice is interesting because it is equivalent to Cardinal Comparability, which seems to be "clearly true"; but also to the Well-Ordering Principle, which seems "clearly false"; and also to Zorn's lemma, which is somewhere in the middle. Most mathematicians now accept the axiom of choice, adding it to the Zermelo-Frankel axioms to give the ZFC system.
We next wonder about consistency itself: it would be great to prove that our ZF axioms are at least consistent if not complete. However, Godel's Second Incompleteness Theorem shows that no consistent system powerful enough to represent arithmetic can prove its own consistency. If it could, then it would be able use the same reasoning that we did in arguing that the self-referential statement from the First Incompleteness Theorem was true, which would make that statement provable after all! We can of course prove the consistency of ZF set theory given some other assumptions - but then we wouldn't be able to prove the consistency of ZF + other assumptions without still more assumptions, and so on (assuming each addition maintains consistency). The best we can hope for here is an appeal to how obvious the axioms are in our universe. In any case, this theorem gives us another example of a (hopefully) true but unprovable statement: the statement of ZF's consistency.
Computability
At this point (in the 1930s) mathematicians were feeling rather dispirited, but there was one last property which they still hoped for: decidability. That is, even though ZF was incomplete, was there any algorithm which would solve Hilbert's "entscheidungsproblem" of deciding in a finite time whether any given statement was provable or not? This problem relied, however, on a definition of algorithm, which was provided independently by Church, Godel and Turing, using entirely different formulations which happened to be equivalent. The equivalence of lambda calculus, u-recursive functions and many different formulations of Turing machines strongly suggests that there is some "natural" divide between questions which can be decided by algorithms and those which can't - and unfortunately for mathematicians, the provability of some mathematical statements is in the latter category. Turing showed this by demonstrating that any algorithm which could figure out whether any Turing Machine halted eventually could produce a contradiction when applied to a version of itself (the role of self-reference in his, Godel's and other impossibility proofs is fascinating!). A follow-up theorem from Rice showed that in fact every non-trivial semantic property of Turing machines is undecidable, because they can be reduced to the halting problem. Turing Machines are limited in other ways too: since there are only a countable infinity of Turing machines and an uncountable infinity of real numbers, "almost every" number is uncomputable, in the sense that there is no Turing machine which outputs it. However, in another sense Turing Machines are an incredibly powerful construction: they can run for arbitrarily long and take up arbitrarily large amounts of space. Further, Universal Turing Machines exist which can simulate any other Turing Machine given to them as input. It is an open empirical question whether or not Turing Machines describe every computation possible in our universe: so far it seems they do, with two caveats. Firstly, Turing Machines are not able to generate true randomness, and so if quantum mechanics is nondeterministic, it could not be implemented using a Turing Machine. However, pseudorandomness is good enough for all practical purposes. Secondly, quantum computers are able to perform some calculations faster than any Turing Machine - but not, it seems, any calculation which a Turing Machine couldn't do eventually.
Since Turing Machines are so important, I'll give a brief sketch of what they are. Turing based his theory of computation on a human mathematician working with pen and paper. The Turing Machine consists of an infinitely long tape, divided into squares which can contain one symbol each - initially they are all empty except for a finite amount of input. There is also a "head" which moves back and forth over the tape one square at a time, reading the symbol there, possibly rewriting it, and possibly changing state. Each state has its own rules for what to do when reading each symbol, and which states it may transition into. Turing argued that because any human mathematician can only distinguish between finitely many symbols, and only remember finitely many things, the symbols and states for each Turing Machine should also be finite. Eventually the Turing Machine may reach a "halting state"; the contents of the tape at that time are the output. Otherwise, the computation may simply never finish. We can relate Turing Machines to mathematics as follows: we define a mathematical system to be a Turing Machine which, given a list of axioms and a mathematical statement (both in L1) either outputs a proof of the statement from the axioms, or else runs forever. Thus we must build the rules of logic into the Turing machine, but the rules of the mathematical system can vary depending on which axioms are used. Of course, from Gödel we know that there are some true statements on which such a machine will run forever.
In fact, using this definition, we can actually come up with more statements which are true but unprovable. Assume that ZF is consistent. Now consider the statement "All Turing machines with n states either halt in fewer than k steps, or run forever." For every value of n, there are only finitely many Turing machines, and so there must be some least value of k for which the statement is true (we assume they start on a blank tape). This value is called the nth Busy Beaver number, or BB(n). But what if n = N, where N is large enough for there to be a N-state Turing machine which searches for a contradiction in ZF by listing all possible proofs and stopping if it finds a proof of a contradiction? Then it cannot halt, because ZF is consistent. But if ZF could prove what BB(N) was, then running it for BB(N) steps without it halting would be a proof that it never halted and that ZF is consistent, which is impossible by Godel's Second Incompleteness Theorem. Thus the value of BB(N) can never be proved in ZF.
What sort of sizes of N are we talking about here? Yedida and Aaronson prove an upper bound on which Busy Beaver numbers can ever be found - it's around 8000 in a variant of ZF which includes a large cardinal axiom. Notice that it must be large enough for a N-state Turing Machine to implicitly encode all the axioms of ZF, plus encode the algorithm for listing and checking all proofs from some axioms. The latter only takes a constant amount of space, and so it turns out that the more compactly our axioms can be encoded, the less we can prove with them! This suggests a fundamental connection between information and proof, one which has been explored in recent decades by the field of algorithmic information theory.
Algorithmic information theory
Algorithmic information theory uses a slightly different convention when it comes to information (following Shannon, who singlehandedly founded information theory in 1948). "Turing Machine states" is not a very natural unit to use for how much information a set of axioms contains; rather, we usually talk about information in terms of "bits". Each bit of information we receive narrows the options we're considering by half. For example, if you wanted to send me a string of 4 binary digits, there are 16 possibilities - but once I receive the first digit, then there are only 8 possibilities left for the remaining 3 digits, so I've received 1 bit of information. Note, though, that "half" is not measured in number of outcomes, but rather in the probability we assign to those outcomes. If I think there's a 50% probability the message will be 0000, 25% probability that it will be 0001, and 25% probability that it will be 1000, then receiving the digit 0 gives me less than 1 bit of information because it only rules out 25% of my initial probability distribution (specificially, it gives me -log(0.75) = 0.415 bits of information). The next two digits I receive will each give me 0 bits of information, and then the last will give me either 0.585 or 1.585 bits depending on whether it's 0 or 1.
This will be confusing for computer scientists, who are accustomed to thinking of each binary digit as 1 bit, regardless of what it is. The distinction to keep in mind is between bits of message, and bits of information. Above, we transmitted 4 bits of message but conveyed only 1 or 2 bits of information because we chose a shoddy encoding which wasted the middle two bits. The distinction makes sense. For example, if you knew I was going to send you a million-bit string of either all 0s or all 1s, then it would contain a million bits of message, but only 1 bit of information: everything after the first digit is redundant. Above we can also see that it's possible for one bit of message to contain more than 1 bit of information; another example would be if you picked a random number between 0 and 1000 and sent it to me using the following encoding: if the number is 20, then send the digit 1, otherwise send 0 followed by the actual number. If I receive a 1, you've ruled out 0.999 of the probability, and given me almost 10 bits of information, with only 1 bit of message. The catch which Shannon proved is that, on average, you can never expect to receive more than 1 bit of information with every bit of message: for every time our unusual encoding scheme saves us effort, there will be 999 times when it adds an unnecessary bit on to the message.
Chaitin has a cool proof of Godel's incompleteness theorem inspired by algorithmic information theory. He notes that Godel's original proof is based on the classic paradox "This sentence is a lie" - except with untruth replaced by unprovability. He bases his proof on another well-known paradox: "The smallest number which cannot be specified in fewer than 100 words." Since there are only finitely many strings of fewer than 100 words, there must be such a number. But whatever it is, we've just specified it in 12 words, so it cannot exist! Formally: given a fixed language, let the complexity of a number be the length of the shortest description of a Turing machine which gives it as output. Consider the number which is defined as follows: search through all possible proofs, in order of length, and identify the ones which demonstrate that a number has a complexity greater than N; output the number which has the shortest such proof. But if N is bigger than the description length required to encode all the axioms and the operating instructions for the Turing Machine I described above, then the program we just described above will have length < N, and so the number we found actually has complexity < N. Contradiction! Therefore we can never prove the complexity of numbers above a certain threshold; and that threshold is based on how many bits of information are contained in the axioms in the language we're using! Chaitin also demonstrated the same idea by formulating "Chaitin's constant", Ω, defined as an exponentially weighted sum of all Turing Machines. Each Turing Machine of length n adds 1/2^n to Ω if it halts, and 0 otherwise. Then Ω can be seen as the probability that a randomly chosen Turing Machine halts. If we know the first K bits of Ω, then we can solve the Halting Problem for all Turing Machines of length < K, by running all other Turing Machines in parallel, adding together the weighted sum of those which have halted, and waiting for that sum to come close enough to Ω that any Turing Machine of length < K halting would push the sum past Ω. Because of this, Ω is uncomputable; further, by a similar argument to the used above with the Busy Beaver numbers, every system of axioms has some upper limit beyond which it cannot determine the digits of Ω. That upper limit is the information content of the axioms, measured in bits, plus a constant which depends on the encoding language we are using.
These results lead Chaitin to a novel view of mathematics. Instead of maths being fundamentally about building up knowledge from axioms, he argues that we should accept that we can prove strictly more if we add more axioms. Therefore mathematicians should behave more like physicists: if there is an elegant, compelling statement which is supported by evidence like numerical checking, but which we haven't been able to prove despite significant effort, then we should simply add it as an axiom and carry on. To some extent, mathematicians have been doing this with the Axiom of Choice, Continuum Hypothesis and large cardinal axioms - the difference is that these are almost all known to be independent from ZF, whereas Chaitin advocates adding working axioms even without such knowledge. Whether or not this is a useful proposal, it is certainly interesting to consider which the major unsolved problems - the Navier-Stokes equations, P = NP, the Hodge Conjecture - may in fact be independent of ZF. And that question brings us to the last part of this discussion, centered around truth in the empirical world.
Truth and Induction
Are our mathematical axioms true? That's a dangerous question. What could it mean, in a universe of atoms and energy, for a mathematical theory to be true? That physical objects obey mathematical rules? We used to think that all objects implemented arithmetic relations: if you have one, and add another, then you end up with two. Now we know that objects are wavefunctions which don't add in such simple ways - and yet nobody thinks that this reflects badly on arithmetic. Is it that physical laws can be very neatly described using mathematics? In that case, what about axioms which aren't needed to describe those laws? Chaitin created a series of exponential diophantine equations which have finitely many solutions only if the corresponding digit of Ω is 0 - so we can never know whether they do or not without many bits of new axioms. But diophantine equations are just addition and multiplication of integers, and surely if anything has some objective truth then it is the outcomes of these basic equations. Now consider a more abstract axiom like the Continuum Hypothesis: either it's true, or it's not true - or we can no longer rely on the logical law of P ∨ ~P. But if it's true, what on earth makes it true? How would the universe possibly be different if it were false? For most of the last two millennia, mathematicians have implicitly accepted Plato's idealisation of numbers "existing" in a realm beyond our own - but with the developments in mathematics that I outlined above, that consensus doesn't really stand up any more. Perhaps we should take Kronecker's intuitive approach - "God made the natural numbers; all else is the work of man" - but if that's true, why does "all else" work so well in physics? On the other hand, Quine advocated only believing in the truth of mathematics to the extent that its truth was a good explanation for our best scientific theories - given current theories, that implies that we should stop roughly at the point where we've derived fields of complex numbers. Even so, what does it mean to believe that the complex or even real numbers "exist"?
I'm going to bow out of answering these questions, because I haven't actually taken any courses on the philosophy of mathematics; I'm hoping that some readers will be able to contribute more. For those interested in exploring further, I recommend a short paper called The Unreasonable Effectiveness of Mathematics in the Natural Sciences. However, now that we've ventured back into the real world, there is one more important issue to discuss: how can we draw conclusions about the world given that, in principle, anything could be possible? We could be in the Matrix - you could all be zombies - the laws of physics could change overnight - the Sun could stop shining tomorrow: these are the problems of induction and skepticism which has plagued philosophers for centuries. In recent decades many philosophers have subscribed to Bayesianism, a framework for determining beliefs which I'll discuss in detail in a forthcoming post. For now, the most important feature of Bayesianism is that it requires a prior evaluation of every possibility, which must give us a consistent set of probabilities, Once we have this prior, then there is a unique rational way to change your beliefs based on any incoming evidence. However, it's very difficult to decide what the prior "should" be - leaving Bayesians in the uncomfortable position of having to defend almost all priors as equally worthy. Enter algorithmic game theory, which allows us to define the prior probability of any sequence of observations as follows. For every Turing Machine of length n, add a probability of 1/2^n to whichever sequence of observations is represented by its output. The sum of all these probabilities for Turing Machines of every length is the unique "rational" prior; the process of generating it is called Solomonoff Induction.
There are three points to make here. The first is that this solution assumes that we should assign probability 0 to any uncomputable observation (which doesn't seem unreasonable); and further, that computable observations should be discounted if they are very complicated to specify. This is an interpretation of Occam's razor - it will give philosophical purists indigestion, but I think we should recognise that going from a broad statement favouring "simplicity" to a precise computational ideal is a clear improvement. Secondly, the exact prior will depend on what language we use to encode observations. There are plenty of pathological languages which artificially place huge probability on very strange outcomes. However, as long as the language is able to encode all possible observations, then with enough evidence ideal Bayesians will converge on the truth. Thirdly, Solomonoff Induction takes infinitely long to compute, so it is only an ideal. Developing versions of it which are optimal given space and time constraints is an important ongoing project pursued by MIRI and other organisations.
That's all, folks. Congratulations for making it to the end; and since you've come this far, do drop me a line with your thoughts :) Answer to the set theory question is ∀x∀y∃z(x∈z ∧ y∈z).

Here is a worthwhile addition. I translated this into Russian in 1992. https://academic.microsoft.com/#/detail/1504169145?FORM=DACADP
ReplyDeletePDF ftp://ftp.cs.utexas.edu/pub/techreports/tr88-09.pdf
ReplyDelete